Cooperation and Defection in Two Social Games

"Game theory is child’s play." –Hoca Camide

Many social interactions involving conflicts of interest can be modeled as simple two-person games where each person, or player, chooses between a prosocial, or cooperating, strategy, and an individualist, or defecting, strategy. Here we take a look at two of the most famous games.

Prisoner’s Dilemma

The prisoner’s dilemma (PD) is surely the most famous of all interpersonal games studied in the social sciences (Poundstone, 1993). It is usually represented by the story of the two prisoners who are separately interrogated by a district attorney who offers them a deal by which they individually benefit from telling on the other while collectively benefitting from remaining silent.

To wit, each suspect is told that if he confesses and betrays the other, while the other does not, he will be set free. If both confess, there will be a penalty of eight years. If, however, neither suspect confesses, they will each receive a penalty of four years. Finally, a suspect who refuses to confess while the other does, ends up with a prison sentence of ten years.

In this game, the refusal to confess amounts to an act of cooperation with the other player, and a confession amounts to an act of defection.

Prisoner's dilemma

Source: J. Krueger

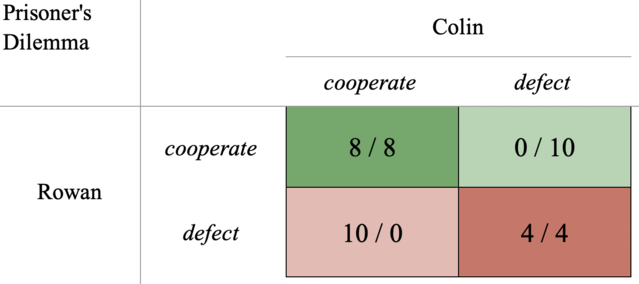
The PD can be more straightforwardly represented with the use of monetary rewards as shown in matrix 1. Let’s call the row player Rowan and the Column player Colin. Their payoffs are respectively shown to the left and to the right of the comma in each cell. Each player is given $4 as an endowment in this “give-some” version of the PD.

If Rowan cooperates by putting his $4 in a pot, he receives $8 if Colin does likewise, but ends up with $0 if Colin defects. If Rowan defects by keeping the money, he receives $10 if Colin cooperates, but wins or loses nothing if Colin also defects ($4). To Colin, the same outcomes apply.

By common notation (Rapoport, 1967), the outcome of mutual cooperation is referred to as R (here $8), unilateral cooperation as S ($0), unilateral defection as T ($10), and mutual defection as P ($4).

The PD is defined by the inequalities of T > R > P > S and it is usually assumed that 2R > (T + S), which means that 2R is payoff-dominant; mutual cooperation yields the largest collective benefit for the two players. Yet, note that each player individually earns more from defection no matter what the other player does. Defection is therefore considered a dominating strategy.

It satisfies the sure-thing principle. If defection beats cooperation if the other player cooperates, and if defection also beats cooperation if the other player defects, then a player should defect even without knowing what the other player has decided to do. However, if both players defect, they individually and collectively fare worse than if both cooperate, and this is the dilemma.

A different way of looking at the dilemma is to consider players’ primary and secondary interests. For each, the primary interest is to have a cooperative partner, as this would yield one of the two highest payoffs ($10 or $8). The secondary interest is to choose defection as one’s own strategy, as this will yield the second-highest pairing of payoffs ($10 or $4). In the same fashion, we may observe that cooperation benefits the other player more than defection benefits the self.

Game of Chicken

The game of chicken (CG) is a game of lesser fame, and it is sometimes confused with the PD. The two games are rarely considered in direct comparison, an omission this essay is meant to address. The CG is marked by the inequalities of T > R > S > P. With a switch of the lower two payoffs, we observe important changes. Although 2R remains the payoff-dominant solution, 2P is no longer the Nash equilibrium it was in the PD. In a Nash equilibrium, neither player has an individual or unilateral incentive to switch strategy. The payoffs shown in matrix 2 make this clear.

Teamwork Essential Reads

How Smart Collaboration Works

Forget Independence: 3 Ways to Teach Children Cooperation

Game of chicken

Source: J. Krueger

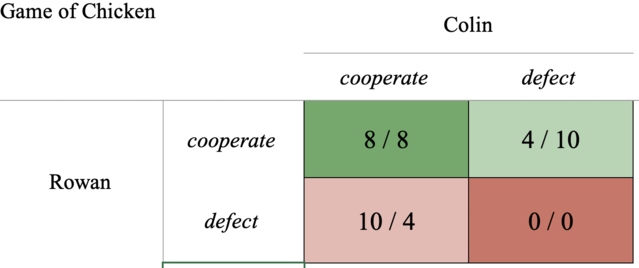
In the CG, it is best to cooperate with a known defector, which turns the outcomes of cooperation-defection and defection-cooperation into Nash equilibria. The trouble is that, since the game demands individual choices without foreknowledge of the other’s choice, a player cannot know if cooperation protects them from mutual defection or if defection will yield the coveted T payoff due to the other’s cooperation, and this is the dilemma.

Cast in terms of interests, we see that each player’s primary interest is, again, the presence of a cooperating partner (yielding either $10 or $8). The secondary, and strategically decisive, interest is to play whichever strategy the other is not playing: defect against a cooperator ($10) but cooperate with a defector ($4).

Since there is no dominating strategy, game theory states that a rational player cooperates with a probability greater than 0. The calculation of this probability is straightforward, although it may require the use of a spreadsheet. Specifically, p = (P – S) / (P + T – R – P) = .5. The effect of the use of p is that the no player has an opportunity to exploit the other as the expected value of cooperation is the same as the expected value of defection.

A Comparison Between Games

According to theory, there should be more cooperation in the CG, where p > 0, than in the PD, where p = 0. Yet, we know that many people cooperate in the PD, and their willingness to do so is predicted by a simple “easiness” index, which Rapoport defined as k = (R – S) / (T – P). This index opens a window into the underlying psychology.

As T – P (the denominator) becomes smaller, defection reduces greed in either game, the index becomes larger, and cooperation more attractive. As P – S becomes smaller, there is less fear of others’ defection, and again cooperation becomes more attractive.

In the games displayed in the matrices, k = .4 for the PD and 1.0 for the CG. That is, the ordering of the payoffs may be enough to increase cooperation in the CG relative to the PD directly, not just the shift in the rational probability of cooperation from 0 in the PD to .5 in the CG.

The confound of p and k is large. If we consider all CG games where T = $10 and P = $0 and vary R and S while maintaining the game-defining inequalities, we find a correlation between k and p of r = .826. To find out if differences in the rational probability of cooperation by themselves increase cooperation, we need to hold game attractiveness k constant.

Here, we can do this by finding a CG with k = 4 so that the PD and the CG share the same level of “easiness,” while differing only in p, the game-theoretical probability of rational cooperation.

We can obtain such a CG by selecting a payoff T for unilateral defection of $24. In other words, we have to considerably increase the appeal of greed in the CG to make the game as unattractive for cooperators as the PD. In this modified CG game p = .2. We can now ask if cooperation is reduced from cooperation seen in the CG game shown in matrix 2 and if it is down to levels seen in the PD shown in matrix 1. If so, then the game-theoretic probability of cooperation has an effect independent of the general attractiveness of the game, that is, its ability to induce greed or fear.

This is a study that – as far as I know – still needs to be run. In the world outside of the lab, a critical challenge for people (i.e., players) is to figure out which type of game, PD, CG, or other, they are in. The researchers who study them face the same challenge.

Alas, games are usually studied in isolation, as if we already knew we all agreed on which game we are playing. Hence, direct comparisons between games are instructive. Such comparisons can be informative about players’ motivations. We might expect that someone who prefers to play a PD is more likely to defect thus revealing greed, and someone who prefers to play a CD is likely more likely to cooperate thus revealing fear of mutual defection.

Which games are you in?