Visualizing Variability: Error Bars in Graphical Displays

Most people have decades of experience looking at graphs. We see them in television reports, books, magazines, presentations at work, and on the stock market apps on our phones.

On the surface, interpreting a graph is straightforward. Does the line go up or down? Is one bar taller than the other? For these simple comparisons, people are intuitive experts in categorizing and drawing inferences about trends and patterns. We naturally compare category sizes to one another (Kosslyn et al., 1977; Tversky, 1977) and attempt to make future predictions based on past performance (Ayton & Fischer, 2004). A new study by Hofman et al. (2020) suggests that one element of how you choose to display data can drastically change how people perceive a treatment.

Relative superiority is rarely all that we want to know from data visualization. Often, we want to know how variable a measure, population, or distribution is. And variability cannot be gleaned from the height of a bar or the slope of a line. Hofman et al.'s study suggests that our ability to interpret variability from data visualization depends on which type of variability is displayed. This new research shows that the error bars that a researcher, CEO, or intern chooses to present can drastically alter the judgments people make about the target measurement.

Before we can dive into the study, however, it is important to consider two ways in which people might choose to display variability. One type of variability we might want to infer from a graph is how likely it is that two populations differ. This is called inferential uncertainty. For example, we might be interested in whether women are higher on extraversion than men. Inferential uncertainty is typically communicated using error bars that correspond to a 95% Confidence Interval or one standard error above and below the mean. The heuristic here is that nonoverlapping error bars imply a statistically significant difference between the two groups. Of course, this inference comes without any indication of the size of that difference.

Alternatively, we may wish to know what the outcome uncertainty is, that is, what the distribution of outcomes looks like around a mean estimate. Here, one might ask: if I were to choose Treatment A over Treatment B, how large is the spread of possible outcomes that I could encounter? Outcome uncertainty can be communicated using error bars that display standard deviations around the mean, or as Hofman et al. used, a 95% prediction interval. This interval corresponds to 1.96 times the standard deviation and tells us that 95 out of 100 observations sampled from this population should fall within the upper and lower bounds.

Now on to the study. Hofman et al. asked whether people would make different judgments about a treatment when viewing inferential uncertainty relative to outcome uncertainty. To do so, they set up a task where online workers were told to imagine competing against an opponent to slide a boulder as far as possible across an ice field. The player who slid their boulder the farthest would win a prize of 250 Ice Dollars, and the loser would win nothing. Participants had to choose whether they would prefer to use the standard boulder (similar to a control condition), or to pay extra money to use a superior boulder that was thought but not guaranteed to be superior (similar to a treatment condition).

Crucially, both the standard and the special boulder varied in their possible outcomes. Participants were shown visualizations of how far each boulder slides on average, but some participants saw graphs with error bars displaying inferential uncertainty (i.e., 95% confidence intervals) and others saw graphs with error bars displaying outcome uncertainty (i.e., 95% prediction intervals, a simple transformation of the standard deviation). Recreations of these visualizations are displayed in the figure below. Keep in mind that these graphs present the exact same underlying data.

The same data displayed using 95% CI (left) and 95% PI (right).

Source: Adapted from Hofman et al. (2020) by Heck, P.R.

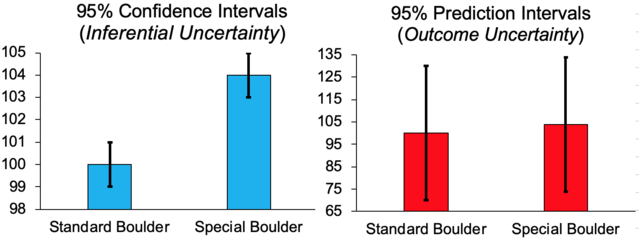
Would this simple change in how variability was displayed—i.e., whether people saw confidence intervals or prediction intervals—affect how much they were willing to pay for the privilege of sliding the special boulder? When the visualization depicted variability using 95% confidence intervals, participants were willing to pay about 60% more for the treatment (about 80 Ice Dollars compared to 50), even though the two visualizations reflected the same underlying data.

In other words, communicating inferential uncertainty by displaying nonoverlapping error bars caused participants to believe that the treatment (the special boulder) was more likely to outperform the control (the standard boulder), relative to those who saw overlapping error bars that display outcome uncertainty. A second study replicated this pattern and explored several other conditions, measures, and visualizations.

Hofman et al.’s study has real-world implications for psychologists, economists, computer and political scientists, and anyone else who uses graphs to communicate data. First and foremost, the type of error bars one chooses to present can drastically affect people’s inferences about the difference between two groups. Choosing confidence intervals or standard errors over prediction intervals or standard deviations, for example, may lead people to overestimate the effectiveness of a medical treatment or the difference between two populations.

Confidence Essential Reads

The Hidden Dangers of Expert Overconfidence

Assumptions That Inhibit Your Confidence and Self-Growth

Conversely, displaying outcome uncertainty may cause people to conclude that an otherwise effective treatment may not be worth pursuing. Psychologists and other scientists almost exclusively publish figures and graphs that display inferential uncertainty to communicate “statistical significance.” It may be worth considering whether simply plotting standard deviations or prediction intervals can give a more realistic picture of the differences in possible outcomes between two groups.

Finally, there are at least two extensions to this study that would be worth pursuing. First, the experimental conditions in Hofman et al. always contained a treatment that was (statistically) significantly superior to the control. But what about situations where one wishes to communicate the absence of a difference between two groups? Non-inferiority trials in medicine, for example, can benefit from visualizations that communicate equivalence between treatment and control as clearly as possible. In the terms of Hofman et al.’s paradigm, how could a visualization most effectively communicate that the “special” boulder is no different from the standard boulder? Here, showing wider bars (i.e., standard deviations) might bias inferences toward equivalence because they make the point-estimates for the means appear closer together.

Second, people often find themselves examining graphs with no error bars at all. The results of political polls, earnings reports, and other charts used outside of the ivory tower often omit uncertainty displays entirely. In order to determine whether confidence intervals or prediction intervals lead to “better” inferences by specialists and the public alike, one should consider a baseline condition that simply shows two bars with no error bars at all. How many Ice Dollars would a person pay to use the special boulder when all she can see is that one bar is taller than the other? Do people infer from the absence of error bars that a result is precise, or perhaps that there is consensus surrounding it? This is an interesting avenue for continued work at the intersection between human judgment and data visualization.