
This essay was written with Emilie Schurenberg -- cooperatively.
Men marry women with the hope they will never change. Women marry men with the hope they will change. Invariably they are both disappointed. ~ Albert Einstein (source)
The simplest way to think about risky choices is to compare their expected values. Suppose you can win $2 (or 2 million) with a probability of .5 or receive $1 (or 1 million) for sure. The expected value of each option is $1 (or a million). A person who only considers these expected values would be indifferent between the two options. Daniel Bernoulli (1954/originally published in 1738) was the first to formally recognize that as values become larger, people become less sensitive to the differences between them. When it comes to money (or other things we consume or enjoy) each additional unit adds less pleasure than the one before. Psychologically, objective monetary value turns into “a perceived subjective, or “utility,” as economists call it” (Stevens, 1975, p. 246). A power function with an exponent of about .5 describes the relationship between value and utility for the average person.
Likewise, people transform objective probabilities into perceived or subjective decision weights. They tend to overweight probabilities below .3 and show little sensitivity to differences among them. Conversely, they treat medium or high probabilities as if they were lower. Kahneman & Tversky (1992) developed prospect theory to account for complex patterns preferences that result from these subjective transformations. When choices refer to possible gains, most people are risk averse unless the probabilities of success are low; in that case, they tend to favor the riskier option. For example, a person faced with a choice between winning 10 million with a probability of .0001 and winning 150 million with a probability of .00000667 may prefer the latter because it is easier to appreciate the difference between the values than the difference between the probabilities, and because the lowest probability is overestimated the most. Yet, the expected value of each option is $1,000. The lack of sensitivity to the differences among very low probabilities may account for the popularity of lotteries with very large payoffs.
As if it weren’t hard enough to comprehend the subjective transformations of values and probabilities, it is even harder, but no less important, to consider situations in which no probabilities are given. Suppose you are in a group of people where each individual can bet on one value. From those who bet on $2, a winner is chosen at random, and likewise for those who bet on S1. Which amount would you bet on? It is not obvious that you should bet on $2. Perhaps everyone bets on 2, which reduces your chances of winning to 1/N, where N is the number of bettors. If you were the one person to switch and bet on 1, you would be sure to get it. But then again, others may have the same idea. The challenge here is not risk but uncertainty. The probabilities of obtaining particular values are not known. While it is reasonable to think that whichever value you select to bet on is also a favorite among other bettors, such projection of one’s choice is maddening. It does not allow you to find a way of placing a bet with a high expectation of winning. If you think others like whatever you like, you will be pessimistic about winning regardless of the value at stake. If so, you might as well bet on the highest one. As we shall see, however, game theorists, who analyze these sorts of situations for a living, have a different idea.
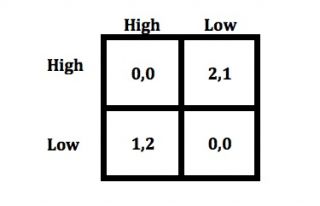
To simplify matters, imagine 2 people, or players: Row and Column. If one bets on High and the other bets on Low, they respectively gain 2 and 1 points. If both bet on the same value, however, neither gets anything. The matrix shows the payoffs. Within each cell, the left value goes to Row and the right value goes to Column.
Game theorists we talked to did not recognize this game by name, but they pointed out that there are three Nash equilibria, that is, combinations of strategies that give no player a reason to switch to a different strategy. Two of these equilibria are pure. If the two players learn that they bet on different values, neither is unhappy and one is very happy. Neither wants to switch lest she’d end up with nothing. The problem with these pure equilibria is that there is no certain way to find them if both players make their bets at the same time and without communicating. Only if Row could move first, she could select High, thus forcing Column to respond with Low. If sequential play is not possible, a mixed equilibrium remains. Each player selects High with the probability that makes the other player indifferent between choosing High or Low. In the present case, that probability is 2/3., and it results in an expected value of 2/3 for each response (High or Low).
This equilibrium is stable but it is not efficient. Players could earn more if they both bet on High with p = .5. The expected value would be ¾, i.e., the average of the expected value of betting on High (1) and the expected value of betting on Low (.5). Game theorists note that a player who bet on High with p = .5 will be exploited by opponents who recognize that by fully switching to High they gain 1 instead of ¾. Meanwhile, the first player’s expected payoff drops to .5. In other words, the efficient solution is desirable but not sustainable.

This game resembles a game called The Battle of the Sexes. In this game, the two players are rewarded if they make the same choice, that is, if they coordinate positively (Luce & Raiffa, 1957, pp. 90-91). Suppose they both prefer going to the opera together but Row loves Wagner whereas Column loves Verdi. The payoffs are displayed in the second matrix. Again, there are two pure equilibria, which are established when both players turn up at the same opera house. Neither has an incentive to switch as that would result in a payoff of zero. The mixed-strategy equilibrium is that each player bets on his or her favorite composer with a probability of 2/3, assuming that one is loved twice as much as the other.
Against the background of this well-known game, the former game might be called The Battle of the Exes (not to be confused with the eponymous MTV show). Both players’ primary objective is not to be in the company of the other. They both like Wagner more than Verdi, but each would settle for Verdi if the other went to Wagner.
Betting on potential monetary payoffs or deciding which opera to see is one thing, reproductive success is another. Before there are exes, there is mating. Consider two men poised to approach two women, one gorgeous and the other just cute. If both men ask the same woman to dance, they block each other (this was dramatized in the movie “A beautiful mind,” which recounted John Nash’s life). If they achieve negative coordination, both men are happy but the man dancing with the gorgeous woman is still happier than the man dancing with the cute woman. Thus, from a male’s perspective the challenge of mate selection bears some resemblance to The Battle of the Exes game. For women the resemblance is weaker because females are more willing to share a mate, especially one with high reproductive fitness. As this fitness is hard to detect, females partly rely on the choices of other females and copy them (see this post).
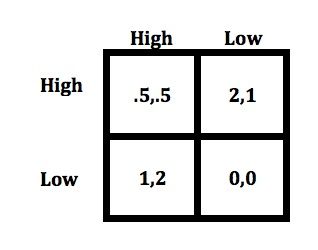
Let’s say females prefer sharing a High male over sharing a Low male, but that they do not like it as much as having a male for themselves. The final matrix displays this situation. Now the mixed equilibrium strategy is to bet on High with a probability of .8.
Bernoulli, D. (1954). Exposition of a new theory on the measurement of risk. Originally published in Latin in 1738. Translation in Econometrica, 22, 23-35.
Luce, D., & Raiffa, H. (1957). Games and decisions: Introduction and critical survey. New York: Wiley.
Stevens, S. S. (1975). Psychophysics: Introduction to its perceptual, neural, and social prospects. New York: Wiley.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297-323.




